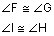Quadrilaterals and Polygons: Trapezoids and Kites

Isosceles Trapezoids

 

Isosceles trapezoids are a special kind of trapezoid in which the two legs are congruent.  They have all the properties of other trapezoids plus the following properties:

    • both pairs of base angles are congruent
    • diagonals are congruent

 

Let’s look at each of these properties.

Base Angles
A pair of base angles are adjacent angles that share the same base.

Take a look at the isosceles trapezoid shown here.

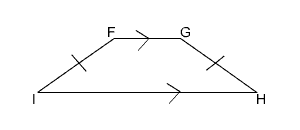
Trapezoid FGHI, with legs FI and GH marked congruent

We can tell that it is an isosceles trapezoid because it has one pair of parallel sides and the legs are congruent.  Angles F and G are one pair of base angles, angles H and I are another pair of base angles.

angle F is congreunt to anlge G; angle I is congruent to angle H

Diagonals

Similar to what we saw in parallelograms, diagonals are drawn from one vertex to the opposite vertex.

Take a look at the diagonals shown here.

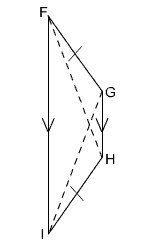
Trapezoid FGHI, with legs FG and IH marked congruent

Because this is an isosceles trapezoid, diagonals FH and GI are congruent.