Properties of Quadrilaterals: Trapezoids
|
A trapezoid is a quadrilateral in which just one pair of sides is parallel. |
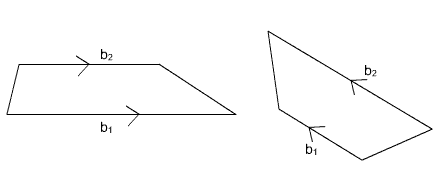
A trapezoid is a quadrilateral in which just one pair of sides is parallel. The parallel sides will be called base one, b1, and base two, b2. Take a look at the following images. Note that the two bases may be horizontal and they may not. They will, however, always be parallel.
|
Properties of all trapezoids include: • adjacent angles not touching the same base are supplementary • length of the midsegment is one-half the sum of the lengths of the bases |
Let’s look at each of these properties.
Adjacent angles in a trapezoid are two angles that are next to each other, but not touching the same base.
Adjacent Angles
The term “adjacent” refers to being next to each other. In this case, we are referring to two angles that are next to each other, but not touching the same base.
Take a look at the trapezoid shown here.
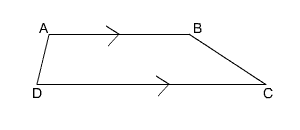
Angle A and angle D are adjacent and touching two separate bases. Angle A and angle D are supplementary.
Angle A and angle B are adjacent but touching the same base. Angle A and angle B are NOT supplementary.
Angle B and angle C are adjacent and touching two separate bases. Angle B and angle C are supplementary.
Angle C and angle D are adjacent but touching the same base. Angle C and angle D are NOT supplementary.
Midsegments
The midsegment is the line segment drawn from the midpoints of each leg.
Take a look at the trapezoid shown here.
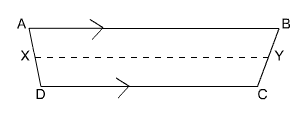
X is the midpoint of leg AD and Y is the midpoint of leg BC. Segment XY is the midsegment.
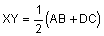
We will look at an example on the next page.