Quadrilaterals and Polygons: Squares, Rectangles and Rhombi

A rhombus is a special parallelogram with the following properties:

Keep in mind that since a rectangle is a parallelogram, it also has all the properties we learned about parallelograms.

Let’s look at a rhombus FGHI and see how the properties can be applied.

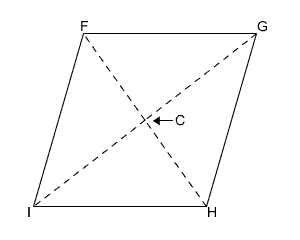
Rhombus FGHI with diagonals intersecting at point C

Example 1
Side GH measures 12x – 21 and side HI measures x + 67. Find the value of x.

One property of rhombi is that all four sides are congruent.

12x – 21 = x + 67
12x = x + 88
11 x = 88
x = 8

Example 2
FH measures 12 and GI measures 16. Find the measure of side FG.

One property of parallelograms, and therefore rhombi, is that the diagonals bisect each other.

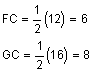
= F C equals one-half the quantity 12 equals 6: G C equals one-half the quantity 16 equals 8

A property of rhombi is that the diagonals are perpendicular. This means that the diagonals create 4 right triangles.

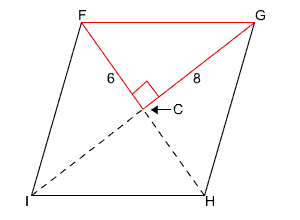
F C equals one-half the quantity 12 equals 6: G C equals one-half the quantity 16 equals 8

We can use the Pythagorean Theorem to find the length of FG.

FG² = 6² + 8²
FG² = 36 + 64
FG² = 100
FG = 10