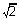Quadrilaterals and Polygons: Squares, Rectangles and Rhombi

Properties of Special Parallelograms: Squares

A square is a special parallelogram with the following properties:

  • All four sides are congruent
  • All four angles are congruent (90°)
  • Diagonals are congruent
  • Diagonals are perpendicular
  • Diagonals bisect each angle


Keep in mind that since a square is a parallelogram, it also has all the properties we learned about parallelograms.

Let’s look at a square KLMN and see how the properties can be applied. 

square KLMN with diagonals intersecting at point C

Example 1
If KL measures 5x – 15 and KN measures 3x + 55, what is the value of x?  What is the length of LM?

One property of squares is that all four sides have equal measure.  We can set these two expressions equal to each other and solve.

5x – 15 = 3x + 55
5x = 3x + 70
2x = 70
x = 35

To find the length of LM we can just find the length of either KL or KN, since all four sides are congruent.

LM = KL = 5(35) – 15 = 160

 

Example 2
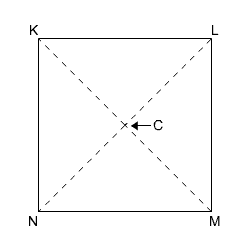
If NL measures 12, what is the length of KL?

The properties of squares are that the diagonals are congruent, perpendicular and bisect the angles.  This means that KM will also measure 12 and that it intersects at a right angle, forming four right triangles.  It also means that the diagonals bisect the 90° angles, creating 45° angles.  One property of parallelograms is that the diagonals bisect each other.  This means that KC measures 6 and CL measures 6.  We have a right triangle with legs both measuring 6.

square KLMN with diagonals intersecting at point C, right triangle KCL highlighted

Recalling what we learned about the special right triangles, we can see that this is a 45°-45°-90° triangle.  The length of KL can be found by taking the leg length, 6, and multiplying by 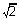square root of two.

KL = 6square root of two