Law of Cosines

The Law of Cosines is another formula to find angle measures or side lengths of a triangle.  It is used when all three side lengths are given, or two sides and the included angle. 

The formula looks similar to the Pythagorean Theorem:

a2 = b2 + c2 – 2bc cos A

 

Remember that the letter names for the angles and sides do NOT have to be a, b and c, so it is important to recognize which sides and angles are used in the formula.

Notice that only one angle is used and it is the angle that is opposite the side length that is on the left side of the equation.

Two other variations of this formula are: b2 = a2 + c2 – 2ac cos B c2 = a2 + b2 – 2ab cos C

Let’s look at how it works.

Example:
Find the length of the missing side in the triangle below.

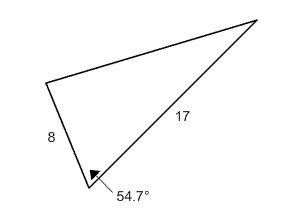Triangle with two sides and the included angle given

 

First of all note that we are given two sides and the included angle.  This is one possible situation when the Law of Cosines works.

Let’s call the missing side ‘a’, which means that .  Again, the actual letters used does not matter, just the fact that the side opposite the known angle is placed on the left side of the equation.

a² = 8² + 17² – 2(8)(17) cos 54.7°
a² ≈ 64 + 289 – 272(0.5779)
a² ≈ 353 – 157.1888
a² ≈ 195.8112
a ≈  
a ≈ 13.99

*Note: when entering this into your calculator, your answers will vary significantly if you round off values throughout the problem.  It is best not to round until the very end of the problem.

Next: Section D, page 10

© 2009 KC Distance Learning. All rights reserved.