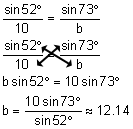Right Triangles and Trigonometry: Law of Sines and Law of Cosines

The Law of Sines

The Law of Sines states that in any triangle the sine of an angle and its opposite side is proportional to the sine of any other angle and its opposite side. 

If the side lengths are a, b, and c and the opposite angles are A, B and C, respectively, then:

the ratio the sine A divided by a equals the ratio the sine B divided by b equals the ratio the sine C divided by c 

Let’s look at how that works.

Example:
Find the length of b.

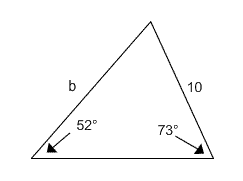Triangle with b opposite an angle with measure 73 degrees and 10 opposite an angle with measure 52 degrees.
Triangle with Two Angles and a Non-Included Side

 

First of all, note that we are given two angles and a non-included side.  This is one of the situations that can be applied to the Law of Sines.

the measure of angle A equals 52 degrees
a = 10
the measure of angle B equals 73 degrees 
b = ?

the ratio of the sine of 52 degrees over 10 equals the ratio of the sine of 73 degrees over b; cross-multiply the ratio of the sine of 52 degrees over 10 equals the ratio of the sine of 73 degrees over b; b times the sine of 52 degrees equals 10 times the sine of 73 degrees; b equals the quotient 10 times the sine of 73 degrees divided by the sine of 52 degrees approximately equals 12 point 1 4 

It is worth noting, that the letters used to represent the sides and angles do not need to be a, b, and c.  What you need to remember is that when setting up the ratios, you should always use the sine of an angle and the side opposite that angle.