Right Triangles and Trigonometry: Law of Sines and Law of Cosines

Law of Sines: More Examples

Let’s look at a couple more examples before you practice on your own.

Example 1:
Find c is the measure of angle C equals 53 degrees , the measure of angle A equals 26 degrees and a = 22.

Solution:

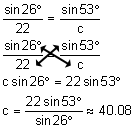
the ratio the sine of 26 degrees over 22 equals the ratio the sine 53 degrees over c: cross-multiply the ratio the sine of 26 degrees over 22 equals the ratio the sine 53 degrees over c: cross-multiply the ratio the sine of 26 degrees over 22 equals the ratio the sine 53 degrees over c: c times the sine of 26 degrees equals 22 times the sine of 53 degrees; c equals the quotient 22 times the sine of 53 degrees divided by sine of 26 degrees approximately equals 40 point zero 8

Example 2:
Find the measure of angle P in the figure below.

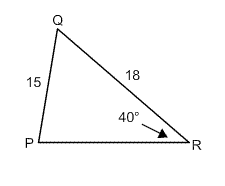Triangle PQR, with side PQ equals to 15, side QR equals to 18 and angle R measuring 40 degrees
Triangle PQR

 

Solution:

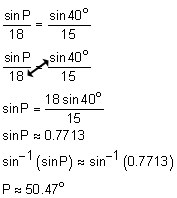
<img src="resources/images/8.4.7_eqtn2.jpg" width="153" height="184" />

*It is worth noting here, that this triangle actually has another possible solution.  You will learn how to find the second solution in future math courses.