Circles: Special Segments in Circles

think icon Think & Click: Properties of Chords

Now, you try. Complete the Think & Click activity by looking at each problem below, thinking about it, and then clicking on the question to reveal the solution.

If the radius of a circle is 31 cm, what is the diameter?
 

d = 2r = 2(31) = 62 cm
 

If the diameter of a circle is 53 in, what is the radius?
 

r equals one-half times d equals one-half times 53 equals 26 point 5
 

Find the value of x.

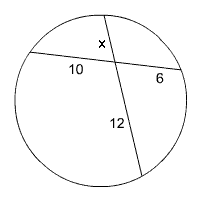Circle with two chords intersecting; one chord has two segments of length 10 and 6, the second chord has two segments of length x and 12
Circle with Intersecting Chords


10(6) = x(12)
60 = 12x
5 = x
 

Find the value of x.

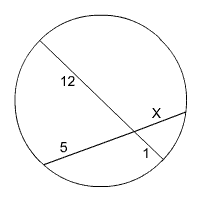Circle with two intersecting chords; first chord has segments of length 12 and 2, second chord has segments of length 5 and x.
Circle with Intersecting Chords


2(1) = 5(x)
12 = 5x
2.4 = x
 

Find the value of a.

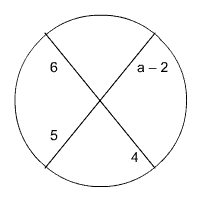Circle with two intersecting chords; first chord has segments of length 6 and 4, second chord has segments of length 5 and a minus 2.
Circle with Intersecting Chords


6(4) = 5(a – 2)
24 = 5a – 10
34 = 5a
6.8 = a
 

In the figure below, PB = PY. If XY = 6 in, what is the length of AC?

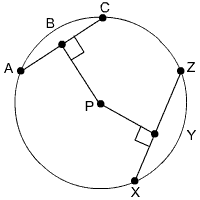Circle P with chord AC, PB is PB is perpendicular to chord AC at point P; chord XZ, PY is perpendicular to chord XZ at point Y
Circle P with Chords AC and XZ


Since PB = PY, we know that AC = XZ.  Since PY is perpendicular to XZ, we know that is bisects it, so XZ = 2XY.
XZ = 2(6) = 12
AC = XZ = 12 inches
 

The diameter of circle C, below, equals 20 cm. HJ = 16 cm. Find the length of CI.

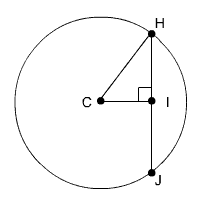Circle C with chord HJ, radius CH and segment CI perpendicular to HJ at point I
Circle C


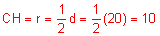
CH equals one-half times d equals one-half times 20 equals 10

Since CI is perpendicular of HJ, it also bisects it. 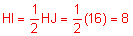the measure of line segment HI equals one-half HJ equals one-half times 16 equals 8

We can use the Pythagorean Theorem with the sides of the right triangle.

CI2 + HI2 = CH2
CI2 + 82 = 102
CI2 + 64 = 100
CI2 = 36
CI = 6 cm