Properties of Tangents
|
Tangents have two main properties:
|
Property 1:
Take a look at the tangent line segment ST.
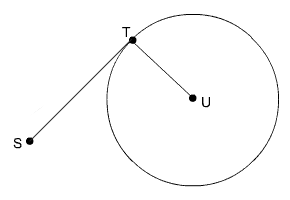
Circle with Tangent ST and Radius UT
The line segment ST is tangent at the point T. According to the first property given, this tangent is perpendicular to radius UT. Angle STU is a right angle. ![]()
Property 2:
Take a look at the two tangent lines draw from point Q.
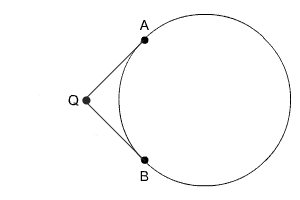
Circle with Tangent QA and Tangent QB