Circles: Special Segments in Circles

think icon Think & Click: Properties of Secants

Now, you try. Complete the Think & Click activity by looking at each problem below, thinking about it, and then clicking on the question to reveal the solution.

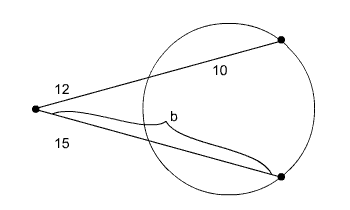
Find the value of b in the image below.

Circle with secants drawn; the first secant has exterior segment equal to 12 and interior segment equal to 10, the second secant has exterior segment equal to 15 and whole segment equal to b
Circle with two secants from the same exterior point

 

12(12 + 10) = 15(b)
12(22) = 15b
264 = 15b
17.6 = b
 

 

Find the value of x in the image below.

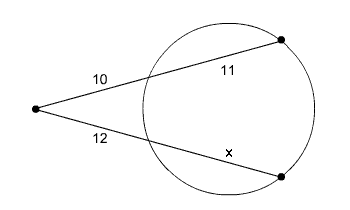Circle with secants drawn; the first secant has exterior segment equal to 10 and interior segment equal to 11, the second secant has exterior segment equal to 12 and interior segment equal to x
Circle with two secants from the same exterior point

 

10(10 + 11) = 12(12 + x)
10(21) = 144 + 12x
210 = 144 + 12x
66 = 12x
5.5 = x
 

 

Find the value of y in the image below.

Circle with secants drawn; the first secant has exterior segment equal to 5 and interior segment equal to 1, the second secant has exterior segment equal to y and interior segment equal to 13
Circle with two secants from the same exterior point

 

5(5 + 1) = y(y + 13)
5(6) = y(y + 13)
30 = y2 + 13y
0 = y2 + 13y – 30
0 = (y + 15)(y – 2)
0 = y + 15 or 0 = y – 2
-15 = y or 2 = y

Since y is a length, eliminate the negative answer.

y = 2