Properties of Secants
The lengths of segments of secants are related in a particular way when the secants intersect outside the circle.
Take a look at the circle and the secants drawn.
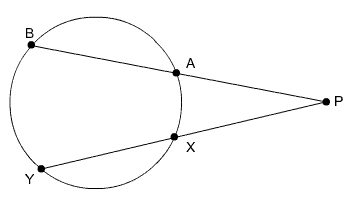
Circle with intersecting secant lines
|
The product of PA times PB equals the product of PX times PY.
|
Example:
What is XY in the figure below?
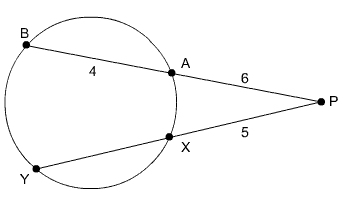
Circle with intersecting secant lines
Solution:
PA = 6
PB = 6 + 4 = 10
PX = 5
PY = 5 + XYPA • PB = PX • PY
6(10) = 5(5 + XY)
60 = 25 + 5XY
35 = 5XY7 = XY