Similarity: Similar Triangles

Similar Triangles Examples

Let’s look at a couple of examples of similar triangles.

Example 1:
These two triangles are similar.

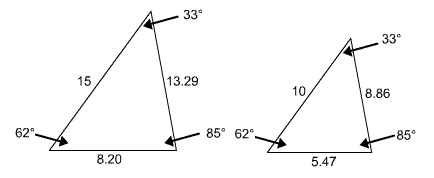First triangle has 62 degree angle, side length 15, 33 degree angle, side length 13.29, 85 degree angle, then side length 8.20; Second triangle has 62 degree angle, side length 10, 33 degree angle, side length 8.86, 85 degree angle, then side length 5.47
Similar Triangles

 

The first property is that corresponding angles are congruent.  Notice that both triangles have angles with measurements of 62°, 33°, and 85°.

The second property is that corresponding sides are proportional.  We will need to check each of the three pairs of corresponding sides.

Side 1: 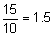fifteen-tenths equals 1 point 5
Side 2: the fraction 13 point 29 over 8 point 86 equals 1 point 5
Side 3:  the fraction 8 point 2 over 5 point 46 equals 1 point 5

 

Notice that the ratios are all equal to 1.5.  The sides, therefore, are proportional.

Example 2:
Are these two triangles similar?

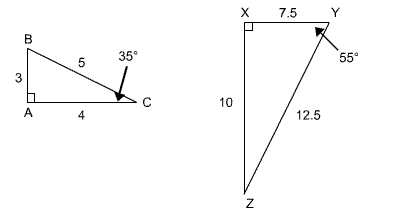Triangle ABC with right angle A, angle C measuring 35 degrees, length of AB equal to 3, length of BC equal to 5, and length of AC equal to 4; Triangle XYZ with right angle X, angle Y measuring 55 degrees, length of XY equal to 7.5, length of YZ equal to12. 5, and length of XZ equal 10
Similar Triangles

 

The first property is that corresponding angles are congruent.

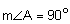
The measure of angle A equals 90 degrees
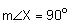
The measure of angle X equals 90 degrees 

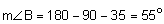
The measure of angle B equals 180 minus 90 minus 35 equals 55 degrees
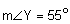
The measure of angle Y equals 55 degrees

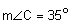
The measure of angle C equals 35 degrees
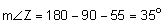
The measure of angle Z equals 180 minus 90 minus 55 equals 35 degrees

The second property is that corresponding sides are proportional. We will need to check each of the three pairs of corresponding sides.

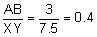
The fraction AB over XY equals the fraction 3 over 7 point 5 equals 0 point 4
The fraction BC over YZ equals the fraction 5 over 12 point 5 equals 0 point 4
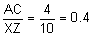
The the fraction AC over XZ equals four-tenths equals 0 point 4

 

Notice that the ratios are all equal to 0.4.  The sides, therefore, are proportional.

Because corresponding angles are congruent and corresponding sides are proportional, the two triangles are similar.

We can writeTriangle ABC is similar to triangle XYZ.  This is read “triangle ABC is similar to triangle XYZ.”  Notice that when the triangles are named, the corresponding angles are in the same order.