Similarity: Similar Triangles

Side-Side-Side Similarity

The second similarity postulate is the Side-Side-Side Similarity Postulate (SSS Similarity Postulate). This states that if the corresponding sides of two triangles are proportional, then the triangles are similar.

Example:
Are the following triangles similar?

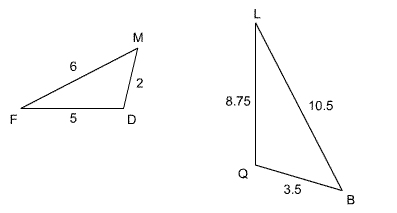First triangle with side lengths MD equals 2, DF equals 5 and FM equals 6; Second triangle with side lengths BQ equals 3.5,QL equals 8.75 and LB equals 10.5

Triangles FMD and QLB

In order to use the Side-Side-Side Similarity Postulate, check the ratios of all three pairs of corresponding sides. The longest side in one triangle always corresponds with the longest side in the other triangle. The shortest side in one triangle always corresponds with the shortest side in the other triangle.

Shortest sides: 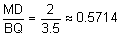$the fraction MD over BQ equals the fraction 2 over 3 point 5 approximately equals 0 point 5714+$
Middle sides: 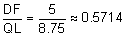$the fraction DF over QL equals the fraction 5 over 8point 75 approximately equals 0 point 5714$
Longest sides: 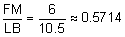$the fraction FM over LB equals the fraction 6 over 10 point 5 approximately equals 0 point 5714$

Since the ratios are all equal, the sides are proportionate and, therefore, by the Side-Side-Side Similarity Postulate, the triangles are similar.