Similarity: Similar Triangles

Side-Angle-Side Similarity

The last similarity postulate we will look at is called the Side-Angle-Side Similarity Postulate (SAS Similarity Postulate). This states that if two sets of corresponding sides are proportional and the included angles are congruent, then the triangles are similar.

Example:
Are the following triangles similar?

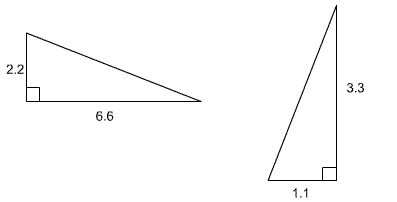First triangle has a right angle with one adjacent side measuring 2.2 and the other adjacent side measuring 6.6; Second triangle has a right angle with one adjacent side measuring 1.1 and the other adjacent side measuring 3.3

Two Right Triangles

In order to use the Side-Angle-Side Similarity Postulate, first check the ratios of two pairs of corresponding sides.

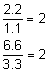
$the fraction 2 point 2 over 1 point 1 equals 2; the fraction 6 point 6 over 3 point 3 equals 2$

Since both ratios equal 2, the two sets of corresponding sides are proportional.

Next, the included angles must be congruent. In the two triangles, the included angles (the angles between the corresponding sides) are both right angles, therefore they are congruent.

The two triangles are similar by the Side-Angle-Side Similarity Postulate.