The Number Line and the Ruler Postulate

A postulate is a statement that is accepted as true and does not need to be proved. For example, we know that under any circumstance, there is at least one point between any two distinct points on a straight line. Think about it.  Between 1 and 2, there is .  Between 1 and is 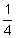, and so on.  Such an observation leads us to develop a postulate called "betweenness”. We use postulates in all of the processes in mathematics, particularly in geometric proofs. You will become familiar and use many of these postulates as you continue working through this course.

A theorem is a statement that can be proven true by undefined terms, definitions, postulates, and other proven theorems.  For example, we know that the diagonals of a rectangle are congruent. This statement has been proven, and you will soon be able to prove this statement as well.

Let’s begin with a postulate about number lines.