Finding Inverse Variation Equations

Finding inverse variation equations is the same as finding direct variation equations, but the general equation is different.

For example, suppose y varies inversely as x, and y = 4 when x = 7, find the inverse variation equation.

The first step is to find k. Use the general equation 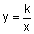and the information given in the problem to solve for the constant of variation.

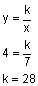
This means that the inverse variation equation is 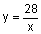.