Prerequisites: Algebra Review

Solving Systems of Equations

If you have two or more unknowns, one equation is not sufficient to find them. In general, if there are n unknowns, you require n equations to solve for them. Typically, to solve for the two unknowns using two equations, solve for one unknown in one equation and substitute it into the second equation. Then, once you have a solution for one value, substitute that back into one of the equations to get the second unknown.

Example

Solve the following pair of equations for x and y.

3x - 2y = 19
x + 4y = -3

To solve for x and y, solve the second equation for x in terms of y and substitute into the second. Then, substitute the value back into one of the original equations to get the solutions.

Solve for x in terms of y in the second equation.
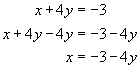x plus four y equals negative three, x plus four y minus four y equals negative three minus four y, x equals negative three minus four y
Substitute the answer from the previous step into the first equation and solve.
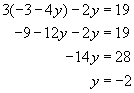three times the quantity negative three minus negative four y end quantity minus two y equals nineteen, negative nine minus twelve y minus two y equals nineteen, negative fourteen y equals twenty eight, y equals negative 2
Substitute the answer from the previous step into one of the equations (choose the simpler of the two equations).
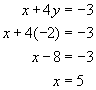x plus four y equals negative three, x plus four times negative two equals negative three, x equals five

The answers are x = 5 and y = -2. You can substitute these values back into the equations to check your work.

There are other ways to solve systems of equations as well, including using your graphing calculator. For more information, reference an algebra textbook or one of the following Web sites. You can also do a search for “systems of equations” in a Web search engine.

**It is a good idea to know how to solve equations and systems of equations although you will be able to use your graphing calculator on the multiple choice section of the AP exam.