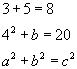Solving Equations
The physical relationships between quantities in physics are described by equations using variables (letters of the alphabet) representing those quantities. Manipulating those variables uses algebra.
An equation is one that has an equals sign in it and it tells you that the quantities on either side of that equals side have the same value. These equations may involve just numbers, just letters (variables), or both.
If you want to solve for one (or more) of the symbols in the equation, we treat that as an unknown. Solving for the unknown variable is also known as solving the equation. In solving, you must find the value of the unknown that satisfies the equation.
![]() Rule for Solving Equations
Rule for Solving Equations
An equation will remain true if any operation performed on one side is also performed on the other side. For example:
- addition or subtraction of a number or symbol
- multiplication or division by a number or symbol
- raising each side of the equation to the same power or taking the same root (such as a square root)
Example
Solve 5f - 7 = 3 for unknown, f
To solve for f, isolate f on the left-hand side of the equation.
Add 7 to both sides |
|
Divide both sides by 5 |
|
Carry out the divisions |