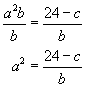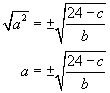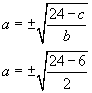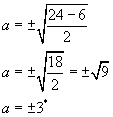Prerequisites: Algebra Review

Self Check Solving Equations Self Check

Now, you try. Complete the self-check activity by looking at the questions below, working them out, and then clicking on the question to review the solution.

think and click icon
Solve for x in the equation 2x + 7 = 15

Perform the same operation on both sides of the equation to isolate x as the only variable on the left side of the equals sign.

Subtract 7 from both sides
two x plus seven minus seven equals fifteen minus seven, two x equals eight
Divide both sides by 2
two x divided by two equals eight divided by two
Carry out the divisions
x equals four

 

think and click icon
Solve the equation a2b + c = 24 for the unknown a in terms of b and c.

We perform operations to isolate a as the only variable on the left side of the equals sign.

Subtract c from both sides.
a squared times b plus c minus c equals twenty four minus c, a squared times b equals twenty four minus
Divide by b.
a squared times b divided by b equals twenty four minus c all over b, a squared equals twenty four minus c all over b
Take the square root of both sides. Remember that when taking the square root there are two possible answers differing only by a + or a -.
square root of a squared equals plus or minus the square root of the fraction twenty four minus c over b, a equals plus or minus the square root of the fraction twenty four minus c over b

 

think and click icon
Solve the equation a2b + c = 24 for the unknown a if b = 2 and c = 6.

If we are given the values, we must plug those values in the place of the variables in the equation.

Use the solution from the previous example and plug the values of b and c into the equation.
a equals plus or minus the square root of the fraction twenty four minus c over b, a equals plus or minus the square root of the fraction twenty four minus six over two
Solve.
a equals plus or minus the square root of the fraction twenty four minus six over two, a equals plus or minus the square root of the fraction eighteen over two equals plus or minus the square root of nine, a equals plus or minus 3

*Whenever we take a square root, the number can be either positive or negative because (-3)2 = 9 just as (+3)2 = 9. In this case, we get two solutions.