Prerequisites: Algebra Review

Quadratic Formula

We sometimes come across equations that have an unknown that appears not only to the first power, but squared as well. Such an equation is called a quadratic equation and can be written in the form ax2 + bx + c = 0. You must use the quadratic formula to solve a quadratic equation for the unknown value.

Key Concept Quadratic Formula

x equals the opposite of b plus or minus the square root of b squared minus four a c all over 2 a note: the opposite of b plus or minus the square root of b squared minus four a c is ALL In the numerator the 2a is the denominator

In the formula, the plus or minus sign indicated that there will be two solutions for x: one where the plus sign is used in the formula and one where the minus sign is used in the formula. Note that the second order equation (raised to the power of 2) has two solutions. Also, the value of b2 - 4ac (the discriminate) must be greater than one to have a real number solution. If it is negative, the value under the square root will be imaginary—and thus the solution will also be imaginary. As you study physics, you will come across some solutions that are imaginary—do not always discard your answer just because you get an imaginary solution!

Sometimes in physical problems one or the other solution may be discarded. You must ask yourself if both solutions make sense in the real-world. Often, a negative answer will be discarded because a negative value makes no sense—take, for instance, when solving for time. A negative time in a physical problem has no real meaning. You will learn more about this concept throughout the course. It is most important that you know how to use and recognize when to use the quadratic formula to find a solution.

Example

Solve 5x2 - 22x - 15 = 0 for x

To solve this equation, use the quadratic formula.

Find the values of a, b, and c.
a equals five, b equals negative twenty two, c equals negative fifteen
Substitute the values into the quadratic formula.
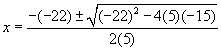x equals opposite of negative twenty two plus or minus the square root of negative twenty two squared minus four times five times negative 15 this is all divided by two times five
Solve the formula using the plus sign.
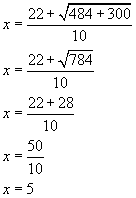x equals twenty two plus the square root of four hundred eighty four plus three hundred all divided by ten, x equals twenty two plus the square root of seven hundred eighty four all divided by ten, x equals twenty two plus twenty eight all divided by ten, x equals fifty divided by ten, x equals five
Solve the formula using the minus sign.
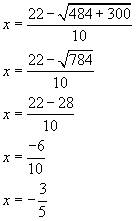x equals twenty two minus the square root of four hundred eighty four plus three hundred all divided by ten, x equals twenty two minus the square root of seven hundred eighty four all divided by ten, x equals twenty two minus twenty eight all divided by ten, x equals negative six divided by ten, x equals negative three fifths

The solutions are x = 5 and x equals negative three fifths