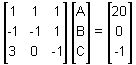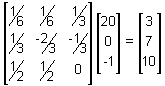Systems of Equations and Inequalities: Systems of Equations with Three Variables

Problem Solving Using Systems of Three Equations

Systems of three equations are used to model many real world situations. The following is an example of one type of problem that is modeled by a system of equations in three variables.

Problem
A triangle has a perimeter of 20 inches.  The length of the longest side is equal to the sum of the lengths of the other two sides.  If you multiply the length of the shortest side by 3 and add 1, the result will be equal to the length of the longest side.  Find the length of each side.

Solution
Before you start, you must define the variables you will use.  For this problem, let’s use A to represent the length of the shortest side, B to represent the length of the second side, and C to represent the length of the longest side.  Now we can use the information given in the problem to write the equations.  Remember that since we have three variables, we must come up with three equations.

The problem says that the triangle has a perimeter of 20 inches.

A + B + C = 20

The length of the longest side is equal to the sum of the lengths of the other two sides.

C = A + B

If you multiply the length of the shortest side by 3 and add 1, the result will be equal to the length of the longest side.

3A + 1 = C

Now that we have three equations, we can set up the matrix equation.  Remember that you must rearrange each equation so that it has the variables on the left and the constant on the right.

A + B + C = 20
-A – B + C = 0
3A – C = -1

This gives us the following matrix equation:

a three by three matrix with the first row: 1, 1, 1; the second row: negative 1, negative 1, 1; and the third row: 3, 0, negative 1; times a three by one matrix with terms A, B C, equals a three by one matrix with terms 20, 0, negative 1

Using technology, find the inverse of the matrix and multiply to find the answer.

a three by three matrix with the first row: one-sixth, one-sixth, one-third; the second row: one-third, negative two-thirds, negative one-third; and the third row: one-half, one-half, 0; times a three by one matrix with terms 20, 0, negative 1, equals a three by one matrix with terms 3, 7, 10

The side lengths are 3, 7 and 10 inches.

When you do these problems, go back and make sure your answer is correct with the description given.