Systems of Equations and Inequalities: Systems of Equations

Solutions to Systems of Equations

One way to solve a system of equations is to graph the lines, and see whether they intersect. If lines intersect at one point, there is one solution to the system of equations. If the lines are parallel, they will not intersect and the system does not have a solution. If you have two of the same line, the graphs will overlap and there are an infinite number of solutions.

The following is the graph of the system of equations:

3x + 2y = 6
x + y = 1

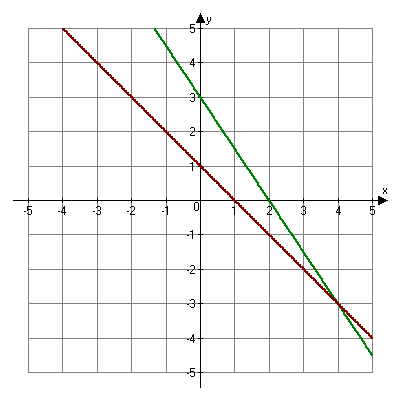
Graphs of three x plus two y equals six and x plus y equals one

Notice that these graphs meet at a single point, (4, -3), and this point is the solution of the system of equations. This system is consistent and independent.

Now look at the graph of the system of equations:

x + y = 3
x + y = -3

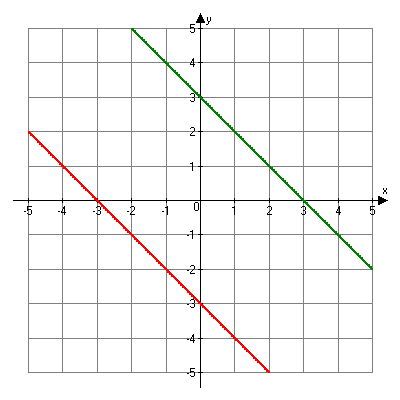
Graph of x plus y equals three and x plus y equal negative three

This system is inconsistent. The two lines are parallel and will never meet. Therefore, this system of equations has no solution.

Finally, analyze the following system of equations:

2x + y = -1
y = -2x – 1

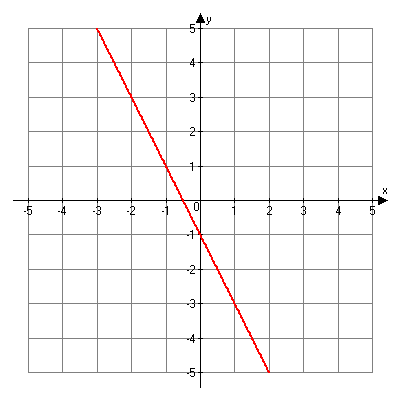
Graph of two x plus y equals negative one and y is equal to negative two x minus one

These lines are exactly the same so they overlap. This means the system of equations has infinite number of solutions and is consistent and dependent.