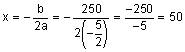Real-World Applications of Min/Max
Maximum and minimum problems can be used to solve real-world situations. One of the most widely known uses of these kinds of problems are optimizations, where some value is maximized. The following is an example of how a maximum value can be used in an optimization problem.
Suppose you want to build a pen with three parallel partitions using 500 ft of fencing. What dimensions will maximize the total area of the pen? Find the area.
The first step is to draw a figure.

We can now write the following formula for the amount of fence that is used:
5(width) + 2(length) = 5x + 2y = 500
We want to use the whole 500 ft of fencing to cover the entire rectangular pen.
Now solve for y.
2y = 500 – 5x
Remember that area is equal to width multiplied by length.
Area = (width)(length) = xy
Find the vertex or the maximum point on the graph.
This means that the dimensions are 50 ft by 125 ft and the area is 6250 ft2.
You will also work on projectile problems and problems when an object is thrown directly into the air. You are working with a quadratic function and the vertex each time, whether it is a maximum or a minimum value.