Surface Area and Volume of A Sphere
|
A sphere is a three-dimensional figure that has cross sections that are circles. All points on a sphere are the same distance from the center of the sphere. |
If you cut straight through a sphere anywhere, the cross section will be a circle as shown in the figure below. Notice that if the cut is made through the center of the sphere, the largest circle is made. This circle has a radius equal to the radius of the sphere.
 |
Sphere with circular cross sections |
I’m sure you can tell by looking at any spherical object (a ball, an orange, a round balloon, etc), that there are no flat sides. In order to find the surface area or volume of a sphere, we will need to use a formula, and as with any formula that involves circles, the number ‘π ’ is included in both.
|
Surface Area of a Sphere: |
If you recall from the last two lessons, surface area is always labeled with units squared. Notice that in this formula, the radius is squared.
|
Volume of a Sphere: |
If you recall from the last two lessons, volume is always labeled with units cubed. Notice that in this formula, the radius is cubed.
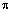 r²;
r²;