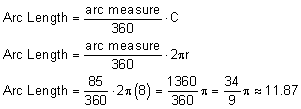Arc Length
We have learned how to find the distance around an entire circle. Now, let’s look at how to find the distance around just part of the circle. When we find just part of the distance around a circle, we are finding arc length.
We can look at part of the circle in a couple of different ways.
First, we can find a fraction of the distance around the circle. For example, we can find one-fourth of the way around, or two-thirds of the way around.
|
To find a fraction of the distance around the circle, simply multiply the fraction by the circumference. |
Example:
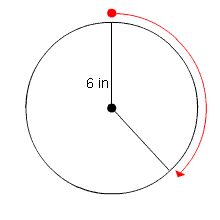
Find the distance around one-third of a circle with radius 6 in.
The Great Pyramid
Solution:
Find the circumference. C = 2πr = 2π(6) = 12π in.
Multiply the fraction by the circumference. ![]()
The distance around one-third of a circle with radius 6 in is 4π in.
The second way we can look at part of the circle is using the measure of the arc. For example, we can find the arc length of an arc with measure 90°, or the arc length of an arc with measure 121°. To do this, we use the arc length formula:
|
|
Example:
Find the length of an arc with measure 85° on a circle with radius 8 ft.
Solution: