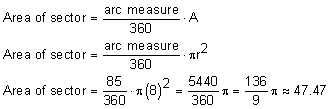Area of a Sector
We have learned how to find the distance around an entire circle. Now, let’s look at how to find the distance around just part of the circle. When we find just part of the distance around a circle, we are finding arc length.
We can look at part of the circle in a couple of different ways.
First, we can find a fraction of the distance around the circle. For example, we can find one-fourth of the way around, or two-thirds of the way around.
|
To find a fraction of the area of the circle, simply multiply the fraction by the area. |
Example:
Find the area of one-third of a circle with radius 6 in.
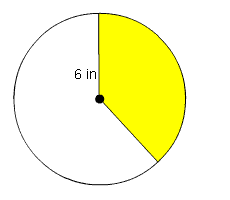
Circle with radius 6 inches
Solution:
Find the area. A = πr2 = π(6)2 = 36π in2.
Multiply the fraction by the area. ![]()
The area of one-third of a circle with radius 6 in is 12π in2.
The second way we can look at part of the circle is using the measure of the arc. For example, we can find the area of a sector with measure 90°, or the area of a sector with measure 121°. To do this, we use the formula for the area of a sector:
|
|
Example:
Find the area of a sector with measure 85° of a circle with radius 8 ft.
Solution: