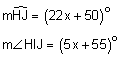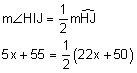Inscribed Angles
|
An inscribed angle is an angle with its vertex on the circle. The measure of an inscribed angle equals one-half the measure of its intercepted arc. The measure of the intercepted arc is twice the measure of in inscribed angle. |
Take a look at circle X below.
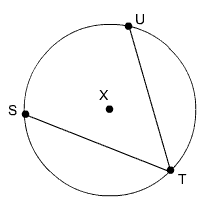
Circle X with inscribed angle STU
If
, then
If
, then
Example:
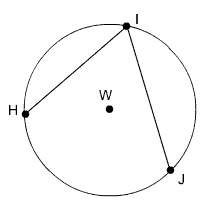
Circle W has the following properties:
Find the value of x.
Solution:
5x + 55 = 11x + 25
5x + 30 = 11x
30 = 6x
5 = x