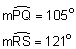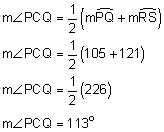Circles: Special Angles and Arcs in Circles

Angles made by Chords, Secants and Tangents

When line segments intersect a circle the intercepted arcs follow certain properties.  When studying these properties, it is very important that you pay close attention to which arcs you are studying.

When two segments intersect in the middle of a circle, the angle at which they intersect is equal to one-half the sum of the intercepted arcs.


Take a look at the image below.

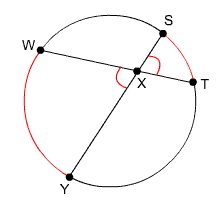
circle with points W, Y, S, and T on the circle; segments WT and SY intersect inside the circle at point X
Circle with intersecting chords

Notice, first that the segments intersect inside the circle. 

The angles marked in red, angleWXY and angleSXT are made by the intersecting segments.  They are vertical angles and therefore have equal measure. 

The arcs marked in red, arc WY and arc ST are the corresponding intercepted arcs.  The measure of the angles equals one-half the sum of the arcs.

the measure of angle WXY equals the measure of angle SXT equals one-half the quantity the measure of arc WY plus the measure of arc ST

Example:
Find the measure of angle PCQ.

the measure of arc PQ equals 105 degrees; the measure of RS equals 121 degrees

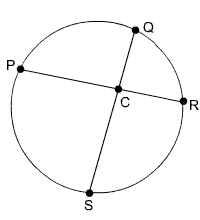
circle with points W, Y, S, and T on the circle; segments WT and SY intersect inside the circle at point X
Circle with intersecting chords

Solution:
First, it is important to notice that angle PCQ is the corresponding angle to intercepted arc PQ and arc RS.

the measure of angle PCQ equals one-half the quantity the measure of arc PQ plus the measure of arc RS; the measure of angle PCQ equals one-half the quantity 105 plus 121; the measure of angle PCQ equals one-half of 226; the measure of angle PCQ equals 113 degrees