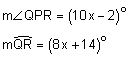Central Angles
|
A central angle is an angle with its vertex at the center of the circle. The measure of a central angle equals the measure of its intercepted arc. |
Take a look at the circle below.
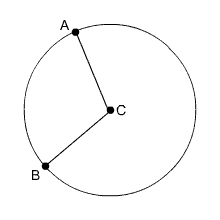
Circle C
If 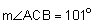 , then
, then 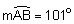 .
.
Example:
Circle P has the following properties:

Circle P
Find the value of x.
Solution:
The measure of the central angle is equal to the measure of its intercepted arc.
10x – 2 = 8x + 14
10x = 8x + 16
2x = 16
x = 8