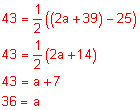Circles: Special Angles and Arcs in Circles

Think & Click: Angles Made by Chords, Secants and Tangents

Now, you try. Complete the Think & Click activity by looking at each problem below, thinking about it, and then clicking on the question to reveal the solution.

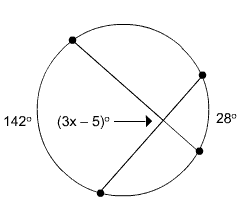
Find the value of x.

Circle with intersecting chords

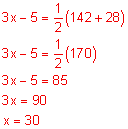
3 x minus 5 equals one-half the quantity 142 plus 28; = 3 x minus 5 equals one-half of 170; 3 x minus 5 equals 85; 3 x equals 90; x equals 30

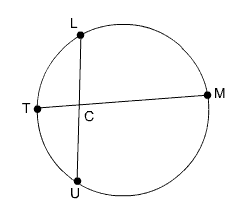
Find the measure of arc LT.

Circle with chords LU and TM that intersect at point C
Circle with intersecting chords

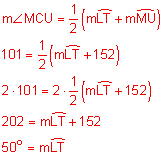
the measure of angle MCU equals one-half the quantity the measure of arc LT plus the measure of arc MU; 101 equals one-half the quantity the measure of arc LT plus 152; multiply both sides by 2; 202 equals the measure of arc LT plus 152; 50 degrees equals the measure of arc LT

Find the value of y.

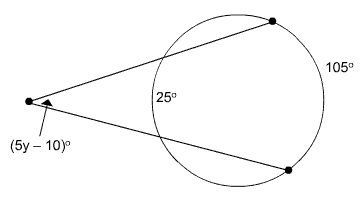
Circle with secants intersecting outside the circle; intercepted arcs measure 105 degrees and 25 degrees; angle of intersection is 5y minus 10 degrees
Circle with secants that intersect outside the circle

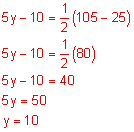
5 y minus 10 equals one-half the quantity 105 minus 25; 5 y minus 10 equals one-half of 80; 5 y minus 10 equals 40; 5 y equals 50; y equals 10

Find the measure of angle J.

Circle with points H, K and F on the circle; tangent line JH and JK
Circle with two tangent lines

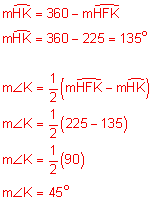
the measure of arc HK equals 360 minus the measure of arc HFK; the measure of arc HK equals 360 minus 225 equals 135 degrees; the measure of angle K equals one-half the quantity the measure of arc HFK minus the measure of arc HK; the measure of angle K equals one-half the quantity 225 minus 135; the measure of angle K equals one-half of 90; the measure of angle K equals 45 degrees

Find the value of a.

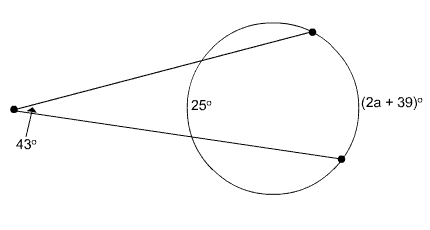
Circle with secants intersecting outside the circle; intercepted arcs measure 2a plus 39 degrees and 25 degrees; angle of intersection is 43 degrees
Circle with secants that intersect outside the circle

43 equals one-half the quantity 2 x plus 39 minus 25; 43 equals one-half the quantity 2a plus 14; 43 equals a plus 7; 36 equals

Complete the review worksheet for this section before taking the quiz. Download the review worksheet, complete the questions, and then download the answer key to check your work. Make sure to ask your teacher any questions.