Ratios

A ratio is simply a comparison of two quantities.  We generally use the word “to” when comparing two quantities.  If we are comparing A and B, we say “the ratio of A ‘to’ B.”

Ratios can be written in several different ways, but they all mean the same thing.

For example, expressing the ratio of boys to girls as "4 to 5" is expressing the ratio in words. Notice that, in the expression "the ratio of boys to girls", "boys" came first. This order is very important, and must be respected: whichever word came first, its number must come first. If the expression had been "the ratio of girls to boys", then the numbers would have been "5 to 4".

There are two other notations for this "4 to 5" ratio:

odds notation:  4 : 5   

fractional notation: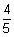

All three notations are interchangeable and you should be able to recognize all of them.

The quantities in a ratio can be multiplied or divided by the same number without changing how they compare.  In other words, in a classroom, there might be 12 boys and 15 girls.  This is still a ratio of 4 to 5.

Ratios are generally written in simplified form.  The actual quantities are simply multiples of these values.  If we say that the ratio of boys to girls is 4 to 5, the actual number of boys is a multiple of 4 (written 4x) and the actual number of girls is the same multiple of 5 (written 5x).

Example:
The ratio of boys to girls at the concert was 4 to 5.  If there is a total of 981 kids at the concert, how many boys and how many girls are there?

Solution:
Boys:  4x
Girls:  5x

4x + 5x = 981
9x = 981
x = 109

Boys: 4x = 4(109) = 436
Girls: 5x = 5(109) = 545

You can always check the result to see if the total matches with what the problem states.  In this case 436 boys plus 545 girls equals 981 kids and .