Using Special Right Triangles
Let’s put all of the information we have leaned thus far to find the cosine and sine of 45°.
We can build the following right triangle:
P(cos 45°, sin 45°)
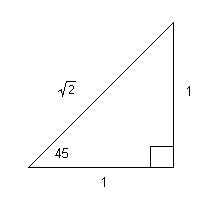
![]()
![]()
You have now found one point on the unit circle.

Let’s put all of the information we have leaned thus far to find the cosine and sine of 45°.
We can build the following right triangle:
P(cos 45°, sin 45°)

![]()
![]()
You have now found one point on the unit circle.
