Quadrant I of the Unit Circle

The following is the first quadrant of the unit circle.

Remember that a unit circle has a radius of 1 unit. The angles in the first quadrant include 30°  or 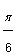, 45° or 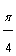, and 60° or 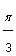. How can we find cosine and sine of these angles using the unit circle?

The answer is that we can build special right triangles. We know that any point P on a unit circle will have an x and a y coordinate. We also know that the x and y values in Quadrant I are both positive. In the case of the unit circle the following is true:

x = cos θ
y = sin θ
and
x² + y² = r² or x² + y² = 1 since the radius of a unit circle is 1. This equation comes from the Pythagorean Theorem.

This means that P(x, y) is equivalent to P(cos θ, sin θ).

Next: Section C, page 7

© 2009 KC Distance Learning. All rights reserved.