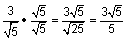Rationalizing the Denominator

There is one more skill that we need to discuss in order to work with the unit circle. It is called rationalizing the denominator. In mathematics, we are not allowed to have a radical in the denominator of a fraction. There is a process called rationalizing the denominator that allows us to remove the radical from the denominator.

For example, if we are given the radical we must rationalize the denominator in order to write the fraction in the correct form. If we multiply the numerator and the denominator by 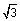we will no longer have a radical in the denominator because we create a perfect square in the denominator.

Let’s try one more example to make sure that we understand the process. Rationalize the denominator of 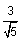. In this case we need to multiply the numerator and the denominator by 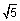in order to remove the radical from the denominator.