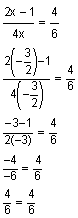Solutions to Rational Equations

Now that you can recognize rational equations, graph rational equations, and find domain and range of rational equations, it is time to solve these types of equations. First, let’s practice checking if a certain value is the solution to a rational equation. We will need the substitution property.

Suppose you have the rational equation and a classmate tells you that he calculated that 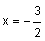. You calculated a different answer so you want to check your friend’s work. Using the substitution property, you can do just that.

Your friend was correct with his calculation. It is important to always check your work when dealing with rational equations. We learned in previous sections that at times we have excluded values that do not work in the equation. You will occasionally come across extraneous solutions which are solutions to an equation that are not solutions to the original equation. Checking your work will help you find these extraneous solutions.