Solving Rational Inequalities Using Algebra
You can also use algebra to solve rational inequalities.
For example, solve 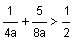 .
.
First rewrite the inequality as 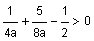 .
.
Next solve for the zeros.
Next find the excluded values. In this case the excluded value is a = 0. This value will make the denominator equal to zero.
Next identify these points on a number line.

Next check values in the three intervals, a < 0, 0 < a < 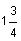 , a >
, a > 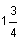 . Pick any value that fits within the interval to see if the inequality holds true. If one value in the interval is true, then all values in the interval will work, and vice-versa.
. Pick any value that fits within the interval to see if the inequality holds true. If one value in the interval is true, then all values in the interval will work, and vice-versa.
|
Try a = -1.
This statement is not true, therefore no values in the interval a < 0 are true.
Next try a = 1. This statement is true. Therefore every value in the interval 0 < a <
Finally, check a = 2. This statement is not true, therefore no values in the interval a > The final answer is 0 < a < |
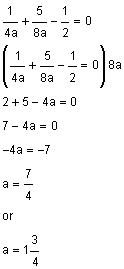
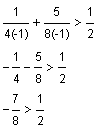

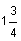 will be true.
will be true.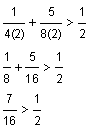
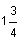 are true.
are true.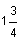 .
.