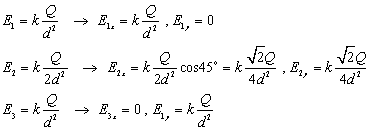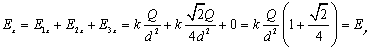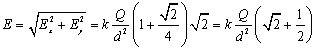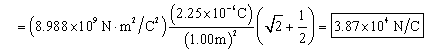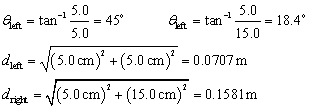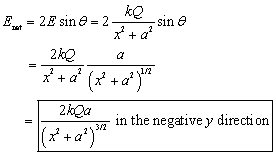Electrostatics: Electric Charges and Fields

Electric Fields

View the following example problem that shows the calculation of an electric field, then, you try some problems.  Complete the self-check activity by looking at the prompts below, working through the problems, and then clicking on the question to review the solutions.

TextbookFor more practice, complete the following problems from Chapter 16 in your textbook. The answers are in the back of your book.

Problems: 23-31 odd

tutorial Tutorial: Electric Fields Example

In this example, you will see an example problem dealing with electric field strength. Select the play button to begin the tutorial, and then use the navigation buttons to pause/stop, continue, or reset the tutorial. View the presentation as often as you would like, and take notes as you follow along. Be sure to set your volume at a reasonable level before you begin.

Download the script as a PDF.

 

Next »

Problem 1

think and click icon
What is the electric field strength at a point in space where a proton m equals 1 point six seven times ten to the negative twenty seventh kilograms. experiences an acceleration of 1 million "g’s"?
Assuming the electric force is the only force on the electron, then Newton’s 2nd law may be used to find the electric field strength.

F sub net equals m a equals q times E which leads to E equals m a over q equals 1 point 6 7 kilograms times 1 times ten to the sixth times 9 point 8 zero meters per second squared divided by 1 point 6 zero 2 times ten to the negative nineteenth Coulombs equals 0 point 1 zero 2 Newtons per Coulomb.

 

« Previous | Next »

Problem 2

think and click icon
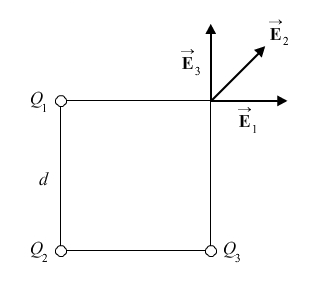
Calculate the electric field at one corner of a square 1.00 m on a side if the other three corners are occupied by 2.25 x 10-6 C charges.

Four charges at the four corners. The charge on the top, right corner has three electric field vectors, each pointing outside the box along a line connecting the charge to the other three charges in the box.

The field at the upper right corner of the square is the vector sum of the fields due to the other three charges. Let the variable d represent the 1.0 m length of a side of the square, and let the variable Q represent the charge at each of the three occupied corners.

E sub 1 equals k times Q over d squared which leads to E sub 1-x equals k times Q over d squared and E sub 1-y equals 0. Equations for charge 2, E sub 2 equals k times Q over 2 d squared which leads to E sub 2-x equals k times Q times cosine of 45 degrees over 2 d squared equals k times square root of 2 times Q over 4 d squared and E sub 2-y equals k times square root of 2 times Q over 4 d squared. Equations for charge 3: E sub 3 equals k times Q over d squared which leads to E sub 3-x equals 0 and E sub 3-y equals k times Q over d squared.

Add the x and y components together to find the total electric field, noting that Ex = Ey.

E sub x equals E sub 1-x plus E sub 2-x plus E sub 3-x equals k times Q over d squared plus k times square root of 2 times Q over 4 d squared plus zero equals k times Q over d squared plus the quantity 1 plus the square root of 2 over 4 end quantity equals E sub y.

The total Energy equation: E equals the square root of the quantity E sub x squared plus E sub y squared end quantity equals k times Q over d squared times 1 plus square root of 2 over 4 end quantity times square root of 2 equals k times Q over d squared times the quantity square root of 2 plus one half end quantity

equals 8 point 9 8 8 times ten to the ninth Newton meters squared over Coulomb squared times 2 point two 5 times ten to the negative sixth Coulombs over the square of one point zero zero meters times the quantity square root of 2 plus one half end quantity equals 3 point 8 seven times ten to the 3 point 8 seven times ten to the fourth Newtons per Coulomb.

Theta equals inverse tangent of the quantity E sub y over E sub x end quantity equals 45 degrees. from the positive x-axis.

 

« Previous | Next »

Problem 3

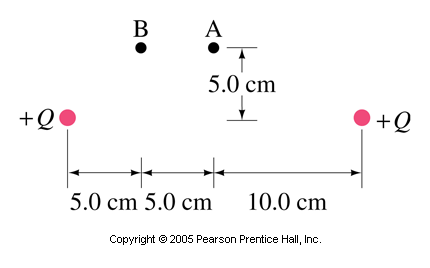
Two charges of positive Q separated by 20 centimeters. Point B is 5 centimeters to the right of the first change and 5 centimeters above the first charge. Point A is midway between the two charges or 10 centimeters to the right of the first charge and 5 centimeters above the first charge.

think and click icon
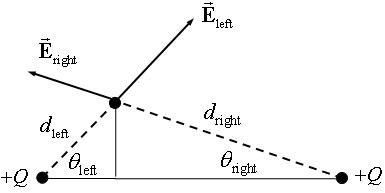
Use Coulomb’s law to determine the magnitude and direction of the electric field at points A and B in the figure due to the two positive charges Q equals seven point zero micro Coulombs. shown. Are your results consistent with the figure?
In each case, find the vector sum of the field caused by the charge on the left Vector E left. and the field caused by the charge on the right Vector E right.

Vector diagram of the Electric fields at point A.

Point A: From the symmetry of the geometry, in calculating the electric field at point A only the vertical components of the fields need to be considered. The horizontal components will cancel each other.

Theta equals inverse tangent of the quantity 5 point 0 over 10 point 0 equals 26 point 6 degrees. D equals the square root of the quantity square of 5 point 0 centimeter plus the square of 10 point 0 centimeters end quantity equals Eleven point one eight centimeters.

Vector diagram of the Electric fields at point B.

Point B: Now the point is not symmetrically placed, and so horizontal and vertical components of each individual field need to be calculated to find the resultant electric field.

Theta left equals inverse tangent of the quantity five point zero over five point zero end equals 45 degrees and theta right equals inverse tangent of the quantity 5 point 0 over 15 point 0 equals 18 point 4 degrees. D sub left equals the square root of the quantity square of 5 point 0 centimeters plus the square of 5 point 0 centimeters end quantity equals 0 point 0 seven zero seven meters. And d sub right equals the square root of the square of 5 point 0 centimeters plus the square of 15 point 0 centimeters end quantity equals zero point one five eight one meters.

 

« Previous | Next »

Problem 4

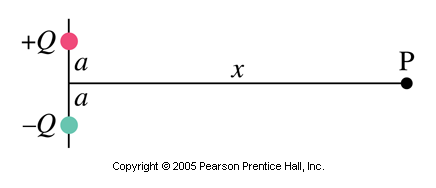
Two charges, one of positive Q a distance a above the x-axis and one of negative Q a distance of a beneath the x-axis. Point P is a on the x-axis a distance x along the x-axis from the other two charges.

think and click icon
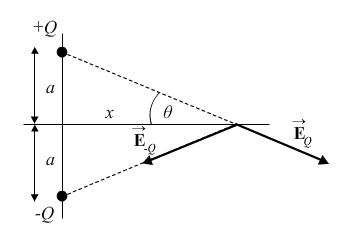
Determine the direction and magnitude of the electric field at the point P shown in the diagram. The two charges are separated by a distance of 2a. Point P is on the perpendicular bisector of the line joining the charges, a distance x from the midpoint between them. Express your answers in terms of Q, x, a, and k.
From the diagram, we see that the x components of the two fields will cancel each other at the point P.

The same diagram as above except now the electric field vectors are shown on point P. One electric field vector points down and toward the negative Q and one field vector points down and away from the positive Q.

Thus the net electric field will be in the negative y-direction, and will be twice the y-component of either electric field vector.

E sub net equals 2 E sine theta equals 2 times k times Q times sine theta over the quantity x squared plus a squared end quantity equals 2 times k times Q over the quantity x squared plus a squared times the fraction a over the quantity x squared plus a squared end quantity to the one half power equals two times k times Q times A over the quantity x squared plus a squared end quantity to the 3 halves power in the negative y direction.

 

« Previous