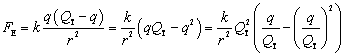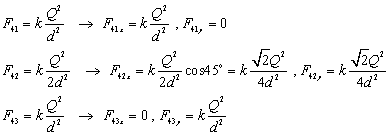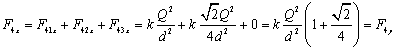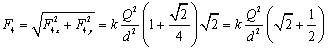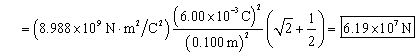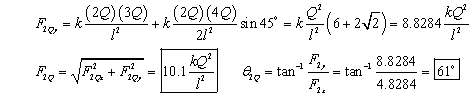Electrostatics: Electric Charges and Fields

self check Coulomb’s Law Calculations Self Check

View the following example problem using Coulomb’s Law, then try a problem on your own.  Complete the self-check activity by looking at the prompts below, working through the problems, and then clicking on the question to review the solutions.

TextbookFor more practice, complete the following problems from Chapter 16 in your textbook. The answers are in the back of your book.

Problems: 1-21 odd (13 is the example below)

tutorial Tutorial: Coulomb’s Law Example

In this example, you will see Coulomb’s Law at work. Select the play button to begin the tutorial, and then use the navigation buttons to pause/stop, continue, or reset the tutorial. View the presentation as often as you would like, and take notes as you follow along. Be sure to set your volume at a reasonable level before you begin.

Download the script as a PDF.

 

Next »

Problem 1

think and click icon
Two positive point charges are a fixed distance apart. The sum of their charges is QT. What charge must each have in order to (a) maximize the electric force between them, and (b) minimize it?
(a) Let one of the charges be q, and then the other charge is QT - q. The force between the charges is:

F sub E equals k times q times quantity Q sub T minus q end quantity over r squared equals k times the quantity q times Q sub T minus q squared end quantity over r squared equals k over r squared times Q sub T squared times the quantity q over Q sub t minus the quantity q over Q sub T end quantity squared end quantity.

If we let x equals q over Q sub t., then F sub E equals k times Q sub T squared times quantity x minus x squared end quantity divided by r squared., where zero is less than or equal to x is less than or equal to one.. A graph of f of x equals x minus x squared. between the limits of 0 and 1 shows that the maximum occurs at x equals zero point five. , or q equals zero point five Q sub T.. Both charges are half of the total, and the actual maximized force is F sub E equals zero point two five times k times Q sub T squared over r squared..

 

« Previous | Next »

Problem 2

think and click icon
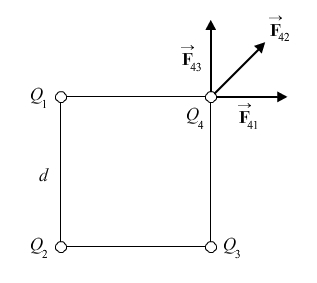
A charge of 6.00 mC is placed at each corner of a square 0.100 m on a side. Determine the magnitude and direction of the force on each charge.

Four charges at the four corners. The charge on the top, right corner has three force vectors, each pointing outside the box along a line connecting the charge to the other three charges in the box.

Determine the force on the upper right charge, and then use the symmetry of the configuration to determine the force on the other three charges. The force at the upper right corner of the square is the vector sum of the forces due to the other three charges. Let the variable d represent the 0.100 m length of a side of the square, and let the variable Q represent the 6.00 mC charge at each corner.

F sub 4-1 equals k times Q squared over d squared leads to F sub 4-1-x equals k times Q squared over d squared, F sub 4-1-y equals zero. F sub 4-2 equals K times Q squared divided by 2-d squared which leads to F sub 4-2-x equals k times Q squared divided by 2-d squared cosine 45 degrees equals k times square root of 2 times Q squared over 4-d squared, F sub 4-2-y equals k times square root of 2 times Q squared over 4-d squared. F sub 4-3 equals k times Q squared over d squared which leads to F sub 4-3-x equals zero, F sub 4-3-y equals k times Q squared over d squared.

Add the x and y components together to find the total force, noting that F sub 4-x equals F sub 4-y.

F sub 4-x equals F sub 4-1-x plus F sub 4-2-x plus F sub 4-3-x equals k times Q squared over d squared plus k times square root 2 times Q squared over 4-d squared plus 0 equals k times Q squared over d squared times the quantity one plus square root of 2 divided by four end quantity equals F sub 4-y.

F sub 4 equals square root of the quantity F sub 4-x squared plus F sub 4-y squared end quantity equals k times Q squared over d squared times the quantity 1 plus square root of 2 over 4 end quantity times the square root of 2 equals k times Q squared over d squared times the quantity square root of 2 plus on half

equals eight point nine eight eight times ten to the ninth Newtons meters squared per Coulombs squared times the quantity 6 point 0 0 times ten to the negative third Coulombs over 0 point 1 0 0 meters end quantity squared times the quantity square root of 2 plus one half end quantity equals 6 point one nine times ten to the seventh Newtons.

theta equals inverse tangent of the quantity F sub 4-y over F sub 4-x end quantity equals 45 degrees. above the x-direction. For each charge, the net force will be the magnitude determined above, and will lie along the line from the center of the square out towards the charge.

 

« Previous | Next »

Problem 3

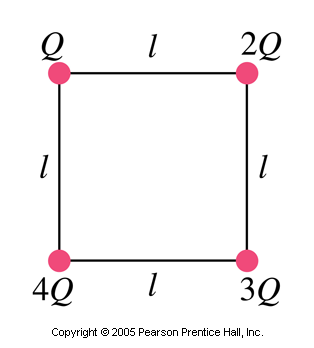
Four point charges, Q, 2Q, 3Q, and 4Q on the four corners of a box clockwise from top-left to bottom-left. The sides of the box are a distance l apart.

think and click icon
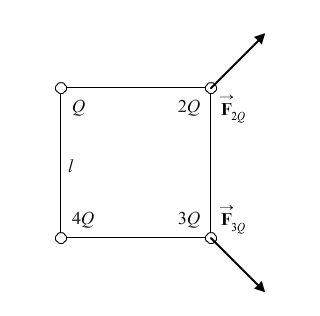
At each corner of a square of side l there are point charges of magnitude Q, 2Q, 3Q, and 4Q. Determine the force on (a) the charge 2Q, and (b) the charge 3Q, due to the other three charges.
Take the lower left hand corner of the square to be the origin of coordinates. Each charge will have a horizontal force on it due to one charge, a vertical force on it due to one charge, and a diagonal force on it due to one charge. Find the components of each force, add the components, find the magnitude of the net force, and the direction of the net force. At the conclusion of the problem is a diagram showing the net force on each of the two charges.

(a)

2 Q calculations as follows: F sub 2-Q-x equals k times two Q times Q over l squared plus k times 2-Q times 4-Q cosine 45 degrees over 2- l squared equals k times Q squared over l squared times the quantity 2 plus 2 square roots of 2 equals 4 point 8-2-8-4 k times Q squared over l squared.

F sub 2-Q-y equals k times 2-Q times 3-Q over l squared plus k times 2-Q times 4-Q times sine 45 degrees over 2-l squared equals k times Q squared over l squared times the quantity 6 plus 2 square roots of 2 equals 8 point 8-2-8-4 times k times Q squared over l squared. F sub 2-Q equals square root of the quantity F sub 2-Q-x squared plus F sub 2-Q-y squared end quantity equals 10 point 1 times k times Q squared over l squared. AND Theta sub 2-Q equals inverse tangent of the quantity F sub 2-y over F sub 2-x equals inverse tangent of 8 point 8 2 8 4 over 4 point 8-2-8-4 equals 61 degrees.

(b)

3-Q calculations: F sub 3-Q-k equals k times 3-Q times 4-Q over l squared plus k times 3-Q times Q times cosine 45 degrees over 2-l squared equals k times Q squared over l squared times the quantity 12 plus 3 fourths times square root of 2 end quantity equals 13 point 0-6-0-7 times k times Q squared over l squared.

F sub 3-Q-y equals negative k times 3-Q times 2-Q over l squared minus k times 3-Q times Q times sine 45 degrees over 2-l Squared equals negative k times Q squared over l squared times the quantity 6 plus 3 fourths times the squared root of 2 equals negative 7 point 0-6-0-7 times k times Q squared over l squared. F sub 3 Q equals the square root of F sub 3-Q-x squared plus F sub 3-Q-y squared equals 14 point 8 times k times Q squared over l squared. Theta sub 3-Q equals inverse tangent of the quantity of F sub 3-y over F sub 3-x equals inverse tangent of the quantity negative 7 point 0-6-0-7 over 13 point 0-6-0-7 end quantity equals 332 degrees.

Four point charges, Q, 2Q, 3Q, and 4Q on the four corners of a box clockwise from top-left to bottom-left. The sides of the box are a distance l apart. On the top-right charge is a force vector pointing out of the box, F sub 2Q, at an angle of 45 degrees. On the bottom-right charge is a force vector point out of the box, F sub 3Q, pointing at an angle of 315 degrees.

 

« Previous | Next »

Problem 4

think and click icon
Two point charges have a total charge of 560 micro Coulombs. When placed 1.10 m apart, the force each exerts on the other is 22.8 N and is repulsive. What is the charge on each?
Since the force is repulsive, both charges must be the same sign. Since the total charge is positive, both charges must be positive. Let the total charge be QT. Then if one charge is of magnitude q, then the other charge must be of magnitude QT - q. Write a Coulomb’s law expression for one of the charges.

F equals k times q times the quantity Q sub T minus q end quantity over r squared which leads to q squared minus Q sub T times q plus F times r squared over k plus zero which leads to q equals Q sub T plus or minus the square root of the quantity Q sub T squared minus 4 F r squared over k end quantity ALL over 2 equals The quantity 560 times ten to the negative sixth Coulombs plus or minus the square root of the quantity of the quantity 560 times ten to the negative sixth coulombs end quantity squared minus 4 times 22 point 8 Newtons times the square of 1 point 1 meters over 8 point 9 8 8 times ten to the ninth Newton meters squared over Coulombs squared end quantity end quantity over 2. The two solutions are 5 point 5 4 times ten to the negative fourth Coulombs and 5 point 5 4 times ten to the negative sixth Coulombs and Q sub T minus q equals respectively 5 point 5 4 times ten to the negative sixth Coulombs and 5 point 5 4 times ten to the negative fourth Coulombs.

 

« Previous