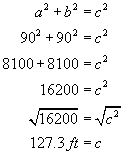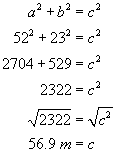Prerequisites: Reviewing Geometry

Right Triangles and the Pythagorean Theorem

A right triangle has one angle that is 90° (a right angle); that is, the two sides that meet at the right angle are perpendicular. The two other (acute) angles in the right triangle add up to 90°.

Pythagorean Theorem

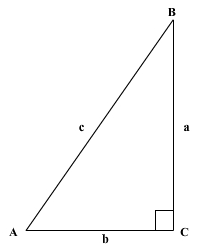
In any right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

a² + b² = c²

A right triangle

Practical Examples

The Pythagorean Theorem is very helpful to solve practical physical problems. Study the following examples carefully to help you apply the Pythagorean Theorem. Notice when we take the square root we only use the positive root. This is because lengths are always positive.

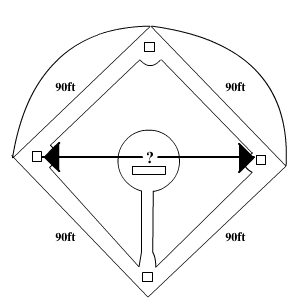
A baseball diamond is actually a square with 90 feet between home and first, first and second, second and third, and fourth and home. What is the shortest distance between first and third base to the nearest tenth of a foot?

a squared plus b squared equals c squared, ninety squared plus ninety squared equals c squared, eight thousand one hundred plus eight thousand one hundred equals c squared, sixteen thousand two hundred equals c squared, square root of sixteen thousand equals square root of c squared, one hundred twenty seven point three feet equals c

A diagram of a baseball diamond.

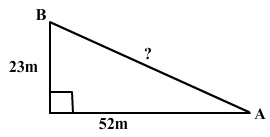
To avoid a pond, Shelly walks directly west 52 meters and then directly north 23 meters. How far would she have had to walk had she been able to cross the pond directly?

a squared plus b squared equals c squared, fifty two squared plus twenty three squared equals c squared, two thousand seven hundred and five hundred twenty nine equals c squared, two thousand three hundred twenty two equals c squared, square root of two thousand three hundred twenty two equals square root of c squared, fifty six point nine meters equals c

A right triangle with legs 52 meters and 23 meters and an unknown hypotenuse.

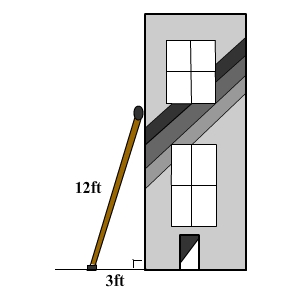
How far up the wall will a 12-foot ladder reach if the recommended distance from the base of the wall is 3 feet?

a squared plus b squared equals c squared, three squared plus b squared equals twelve squared, nine plus b squared equals one hundred forty four, b squared equals one hundred forty four minus nine, square root of b squared equals square root one hundred thirty five, b equals eleven point six feet

A ladder leans against a wall making a right triangle with the wall, the ground, and the ladder.