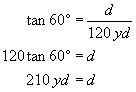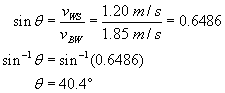Prerequisites: Reviewing Geometry

Self Check Self Check: Trigonometric Ratios

Now, you try.  Complete the self-check activity by looking at the prompt below, working through it, and then clicking on the question to review the solution.

think and click icon
Jean camps beside a wide river and wonders how wide it is. She spots a large rock on the bank directly across from her. She then walks upstream until she judges that the angle between her and the rock, which she can still see clearly, is now at an angle of 30° downstream. Jean measures her stride to be about one yard long. The distance back to her camp is 120 strides. About how far across is the river in meters?

Consider the diagram shown.  L is the distance she walks upstream, which is about 120 yards.  Find the distance across the river from the diagram.

tangent of sixty degrees equals d divided by one hundred twenty yards, one hundred twenty times tangent of 60 degrees equals d, two hundred ten yards equals d

Then, find how many meters are in 210 yards:

two hundred ten yards times three feet divided by one yard times zero point three zero five meters divided by one foot equals one hundred ninety meters

Jean is at the right angle of a right triangle. The longer leg is from Jean to the rock across the river the shorter leg is 120 strides downstream and the angle of sight after walking down is 30 degrees.

think and click icon
A boat’s speed in still water is 1.85 m/s. If the boat is to travel directly across the river whose current is 1.20 m/s, at what upstream angle must the boat head?

In this case, you know the length of one of the sides (speed of the water with respect to the shore) and the hypotenuse (speed of the boat with respect to the water) of the triangle and you need to find the angle theta from the diagram. Use the sine ratio to find the angle measure (if you are using a calculator, make sure that “angle” is set to “degrees” in the setup).
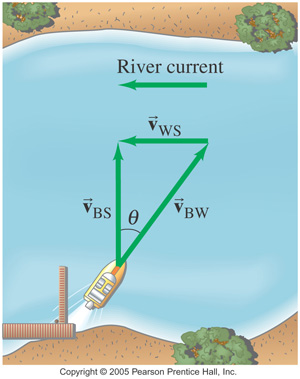
A river is shown with the current going downstream. A triangle is shown with vectors. The velocity vector downstream and the velocity vector of the boat traveling directly across the river meet and form the right angle. The velocity vector showing the direction the boat is pointed forms the hypotenuse.
To move directly across the river, the boat must head upstream at an angle Θ. Velocity vectors are shown as green arrows