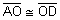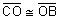Geometry: Geometry of Quadrilaterals

Properties of Parallelograms

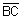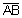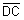Let’s begin our discussion of the Geometry of quadrilaterals with parallelograms. A parallelogram is a quadrilateral with both pairs of opposite sides parallel. For example, ABCD is a parallelogram with line segment B C || line segment A D and line segment A B || line segment D C . Remember, the symbol || means parallel.

Parallelogram ABCD with diagonals AC and DB that meet at point O.

The following is a review of the properties of parallelograms from Geometry.

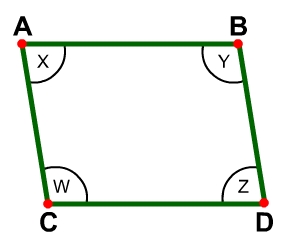
Properties of the Angles of Parallelograms

ABDC is a parallelogram with angles X, Y, Z, and W.

Parallelogram ABDC with angles X, Y, Z, and W

Angles X and Z are opposite.
Angles W and Y are opposite.
Opposite angles of a parallelogram are congruent.

Consecutive angles are next to each other or adjacent.
Angles X and Y are consecutive angles.
Angles Y and Z are consecutive angles.
Angles Z and W are consecutive angles.
Angles W and X are consecutive angles.
Consecutive angles of a parallelogram are supplementary. Recall, supplementary angles have a sum of 180 degrees.

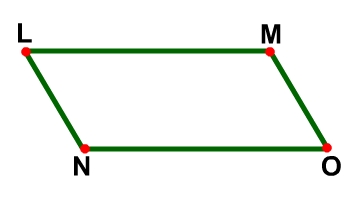
Properties of the Sides of a Parallelogram

LMON is a parallelogram.

Parallelogram LMON

The opposite sides of a parallelogram are congruent.
Sides LM and NO are congruent.
Sides LN and MO are congruent.

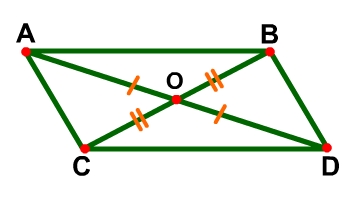
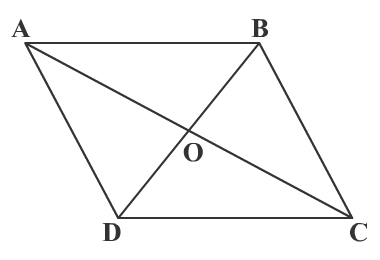
Properties of the Diagonals of a Parallelogram

ABDC is a parallelogram with diagonals AD and BC that meet at point O.

Parallelogram ABDC with diagonals AD and BC that meet at point O

The diagonals of a parallelogram bisect each other.