Determinant of a Matrix
The determinant of a square matrix (one that has the same number of rows as columns) is a real number that can easily tell us whether or not a matrix has an inverse. The inverse will be vital when we use matrices to solve equations in upcoming sections.
Let A =  . The determinant of A, denoted det(A) or
. The determinant of A, denoted det(A) or 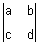 is defined at det(A) = ad – bc.
is defined at det(A) = ad – bc.
Matrix A has an inverse if and only if it is square and det(A) ≠ 0.
For example, given the A =  , det(A) = ad – bc = 3(2) – 6(5) = 6 – 30 = -24.
, det(A) = ad – bc = 3(2) – 6(5) = 6 – 30 = -24.
Because this does not equal 0 and matrix A has the same number of rows as columns, matrix A has an inverse.