Graphing Square Root and Cube Root Functions
Now that you have gone through the values of "a", "b", "h", and "k", work through some examples.
Name the translations of the function ![]() and graph the function.
and graph the function.
The first thing that you should notice is that this isn't written exactly in ![]() form. You need to factor the b out of the expression –x + 3.
form. You need to factor the b out of the expression –x + 3.
-x + 3 = -1(x – 3)
Now you can rewrite this function as ![]() .
.
You can now identify the translations:
a = 2
Vertical stretch by a factor of 2.b = -1
Reflection across the y-axis.h = 3
Horizontal translation of 3 units to the right.k = -1
Vertical shift of 1 unit down.
You are ready to graph the function. The green graph is of the parent function ![]() . The red graph is of your transformed function
. The red graph is of your transformed function ![]() .
.
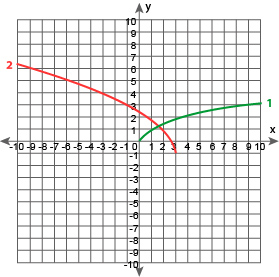
Graph of ![]() and
and ![]()