Radical Functions: Graphing Radical Functions and Domain and Range

The Square Root and Cube Root Parent Functions

In the warm-up you reviewed how the values of "a", "h", and "k" affected the parent function y = x2. There are two more parent functions that you need to go through.

The first is the square root function. Make a table and fill in the x- and y-values so that you can graph the function f of x equals the square root of x .

x
f(x)
1
1
4
2
9
3
16
4

Why doesn’t this table include negative values of x? Remember that when you have a negative inside a square root, your solution will include an imaginary number. You are only interested in real solutions for this graph.

Plot the points on the coordinate plane and draw the graph of f of x equals the square root of x.

Graph of f of x is equal to square root of x starting at (0, 0) with points (1, 1), (4, 2), and (9, 3) shown.
f of x equals the square root of x

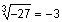You can create a similar table for f of x equals the cube root of x. One important thing to remember is that cube root functions can have a negative as a radicand. For example, the cube root of negative twenty seven equals negative three since negative three times negative three times negative three equals negative twenty seven. As a general rule all odd roots can have negative radicands while all even roots will have imaginary answers if the radicand is negative.

x
f(x)
-8
-2
-1
-1
0
0
1
1
8
2

Plot the points on the coordinate plane and draw the graph of f of x equals the cube root of x.

Graph of f of x is equal to the cube root of x with points (negative 8, negative 2), (negative 1, negative 1), (0, 0), (1, 1), and (8, 2) shown.
f of x equals the cube root of x