The Pythagorean Theorem
|
The Pythagorean Theorem is used to relate the side lengths of a right triangle. It states that the sum of the squares of the lengths of the legs of a triangle is equal to the square of the length of the hypotenuse. If a and b represent the lengths of legs and c represents the length of the hypotenuse, the following is the relationship: a2 + b2 = c2 |
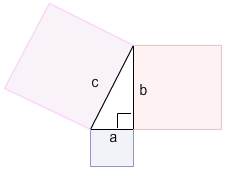
The Pythagorean Theorem
Any three integers that satisfy the Pythagorean Theorem are called a Pythagorean Triple.
Example:
Do the lengths 15, 36, and 39 make a right triangle?
Solution:
First, recognize that 39 is the longest length, so that must be the length of the hypotenuse, or c. Check to see if the side lengths make the Pythagorean Theorem equation true.
a2 + b2 = c2
152 + 362 = 392
225 + 1296 = 1521
1521 = 1521
Because the equation is true, the side lengths 15, 36, and 39 do make a right triangle. Since these values are integers and they satisfy the Pythagorean Theorem, they are considered a Pythagorean Triple.
Example:
Do the values 0.6, 1.0, and 0.8 satisfy the Pythagorean Theorem?
Solution:
To test to see if they satisfy the Pythagorean Theorem, substitute them into the equation and see if the equation is true. The length 1.0 is the longest length, so that must be the value of c.
a2 + b2 = c2
0.62+ 0.82 = 1.02
0.36 + 0.64 = 1.0
1.0 = 1.0
The values satisfy the Pythagorean Theorem, which means they would make a right triangle. Since they are not integers, they are not considered a Pythagorean Triple.