Transformations of Trigonometric Functions

Like linear, quadratic, square root, cube root, exponential and logarithmic functions, trigonometric functions can be transformed. The general formulas are as follows:

y = asin(x – h) + k
y = acos(x – h) + k
y = atan(x – h) + k

For trigonometric functions, "a" is equal to the amplitude.

Amplitude = (maximum value – minimum value)

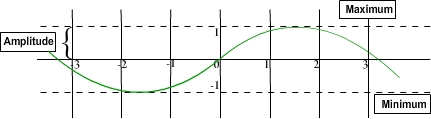
Analyze the following graph. Notice the maximum and minimum values and the amplitude. If you take the maximum value of 1 and subtract the minimum value of -1 you will have 2. Divide this number by 2 and you have an amplitude of 1.

The "h" value is a horizontal translation of the graph. This is also called a phase shift. Again, if
h < 0 the shift is h units to the left. If h > 0 the shift is h units to the right.

The "k" value is a vertical translation. If k > 0 the translation is up k units. If k < 0 the translation is down k units.

Next: Section E, page 6

© 2009 KC Distance Learning. All rights reserved.