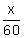Angle of Elevation
We can now apply the right triangle trigonometry that we have learned to solve real-world problems. The first thing that we need to discuss is called the angle of elevation.
Analyze the following diagram.
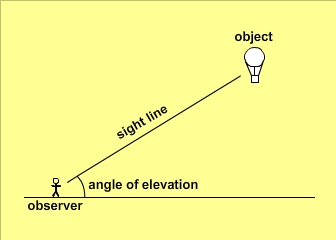
The angle of elevation is the angle between the horizontal line and the line of sight to an object above the horizontal line.
Let’s look at the following example.
An engineer is surveying a building with a device that is 10 feet above the ground. He is 60 feet from the building and is looking with an angle of elevation of 45°. How tall is the building?
The first step is to draw a diagram.
Now set up a trigonometric equation given the information in the problem.
tan 45° =
Solve for x.
This is not the entire height of the building. You still need to add 10 feet since the surveyor is looking at the building 10 feet off the ground. Therefore, the building is 70 feet tall.x = 60(tan 45°)
x = 60 ft.