Rational Functions: Graphing Rational Functions and Domain and Range

section warm up Section Warm-Up

In the previous section you learned about the general forms of direct and inverse variation equations and how they look graphically. Before beginning our work in this section, let’s take a closer look at the inverse variation equation. The following is the graph of y equals 1 divided by the sum of x plus 3, plus 1.

Graph of y equal to one divided by the quantity x plus three plus one, x equals negative three, and y equal one.
y equals 1 divided by the sum of x plus 3, plus 1

Notice the two green dashed lines in the graph. What do you think those represent? These lines are called vertical and horizontal asymptotes.

Vertical Asymptote

Vertical asymptotes are lines where the graph is undefined. Take a look at x = -3:

y equals 1 divided by the sum of x plus 3, plus 1

y equals 1 divided by the sum of negative 3 plus 3, plus 1, y equals 1 divided by 0, plus 1

When x = -3 the denominator of the equation is zero which is not allowed. This means x = -3 is an excluded value, which is represented by a vertical asymptote.

Horizontal Asymptote

Horizontal asymptotes are lines that the graph approaches as x gets larger and larger in either the positive or negative direction.

Take a look at the values of the function as x gets larger in the positive direction :

x 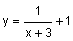y equals 1 divided by the sum of x plus 3, plus 1
10 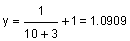y equals 1 divided by the sum of 10 plus 3, plus 1 equals 1.0909
100 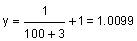y equals 1 divided by the sum of 100 plus 3, plus 1 equals 1.0099
1000 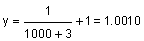y equals 1 divided by the sum of 1000 plus 3, plus 1 equals 1.0010
10,000 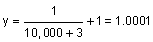y equals 1 divided by the sum of 10,000 plus 3, plus 1 equals 1.0001

Notice that the value of y is approaching 1.


Now take a look at the values of the function as x gets larger in the negative direction :

x 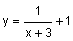y equals 1 divided by the sum of x plus 3, plus 1
−10 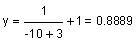y equals 1 divided by the sum of negative 10 plus 3, plus 1 equals 0.8889
−100 y equals 1 divided by the sum of negative 100 plus 3, plus 1 equals 0.9899
−1000 y equals 1 divided by the sum of negative 1000 plus 3, plus 1 equals 0.9990
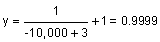−10,000 y equals 1 divided by the sum of negative 10,000 plus 3, plus 1 equals 0.9999

Notice, again, that the value of y is approaching 1. Since the value of y is approaching 1 as x gets larger and larger, the line y = 1 is a horizontal asymptote.

 

Keep this discussion of asymptotes in mind as we start to graph rational functions and find the domain and range of these functions.