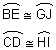Chords of Circles
Suppose you have two congruent circles, A and F, which have two sets of congruent arcs.

Find x and y.
Another property of circles is that if you have congruent circles, any chords that are drawn which intercept congruent arcs will be congruent. We are told that circles A and F are congruent. Because arc BE is congruent to arc GJ, segment BE is congruent to segment GJ. Because arc CD is congruent to arc HI, segment CD is congruent to segment HI.
Since the chords are congruent, we can write the following two equations.
x – y = 3
7x – y = 9
We now have a system of equations which we are familiar with. Let’s solve this system of equations by substitution. Begin by solving the first equation for x.
x = y + 3
Next substitute this equation into the second.
7(y + 3) – y = 9
7y + 21 – y = 9
6y + 21 = 9
6y = -12
y = -2
Next, solve for x by substituting y = -2 into the first equation.
x – (-2) = 3
x + 2 = 3
x = 1
You final answer is x = 1 and y = -2.
Keep in mind that this property only applies when the circles are congruent.