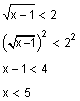Solving Radical Inequalities
Now that you have a good grasp of how to solve radical equations, let's move on to radical inequalities. Let's work through an example as we learn about solving radical inequalities.
Solve ![]() .
.
One of the first things that you need to remember is that anything inside the radical sign of a square root function must be greater than or equal to zero.
In this case x – 1 ≥ 0 so x ≥ 1. If this is not true then our whole inequality is false.
The next step is to solve the original inequality.
The next step is to graph these two statements on a number line. Remember, these two statements are linked by an "and". Both must be true in order for the inequality to be true.
x ≥ 1 and x < 5
![]()
The final answer is x ≥ 1 and x < 5 or 1 ≤ x < 5.
Let's analyze a table of values for this function:
x
0
Undefined
1
0
2
1
3
1.4
4
1.7
5
2
6
2.2
The values of x = 1, x = 2, x = 3, and x = 4 all have f(x) values that are less than 2, which is the inequality that must hold true for our problem. When we get to x = 5 and all x values larger that
x = 5, the f(x) value is greater than or equal to 2. Analyzing this graph can show you another way of reaching the final solution of x ≥ 1 and x < 5 or 1 ≤ x < 5.